Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam
X and the City: Modeling Aspects of Urban Life (51 page)

For Bessel cities, both the density and rental are oscillatory and vanish infinitely often as the distance from the center increases indefinitely. Furthermore, the model predicts that the population density can become negative. Obviously this cannot be the case in reality, so it makes sense to define a
finite Bessel city
by truncating the model at the first zero of the corresponding Bessel function. It is interesting to note that in his
α
= 1 models, Amson (1972, 1973) identifies the positive but ever-decreasing peaks in the Bessel function as “satellite town belts” surrounding a central city, with the regions of negative density identified as greenbelt regions. If the first zero of
J
0
(
r/β
) occurs at
r
=
R
1
, the area of this can be called the central area, with central population
M
(
R
1
). The zeros of Bessel functions are tabulated and available online. Since the first zero of
J
0
(
x
) occurs when
x
≈ 2.405, it follows that
R
1
≈ 2.405
β
= 2.405(
A/πk
)
1/2
. Hence the central area is
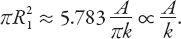
From this simple result we see that it depends directly on the rental coefficient
A
and inversely on the coercion coefficient
k
, but is independent of the central density
ρ
(0). It can also be shown that for given values of
A
and
k
the central rental
P
(0) varies as the square of the central population.
SCALING IN THE CITY

=
r
(
n
): SIZE OF THE CITY
No, by “scaling in the city” we don’t mean what Spiderman does in his various movie adventures . . . There is, according to Brakman et al. (2009, available in Oxford’s online resource center),
a remarkable regularity in the distribution of city sizes all over the world, also known as the “Rank-Size Distribution.” Take, for example, Amsterdam, the largest city in the Netherlands and give it rank number 1. Then take the second largest city, Rotterdam, and give it rank number 2. Keep on doing this for those cities for which you have data available, possibly selecting only cities exceeding a certain minimum
size. If you calculate the natural logarithm of the rank and of the city size (measured in terms of the number of people) and plot the resulting data in a diagram you will get a remarkable log-linear pattern, this is the Rank-Size Distribution. If the slope of the line equals minus 1, as is for example approximately the case for the USA, India, and France, the relationship is known as Zipf’s Law.
This means that the largest city is always about twice as big as the second largest, three times as big as the third largest, and so on, in approximate inverse proportion to its rank. Mathematically, if we rank cities from largest (rank 1) to smallest (rank
N
) to get the rank
r
(
n
) for a city of size
n
, then log
r
(
n
) = log
A
+
a
log
n
, or equivalently
r
(
n
) =
An
a
, where the parameters
A
and
a
are chosen to fit the data. This power law is called an
allometric
relationship (allometry is the study of the change in proportion of parts of an organism as a consequence of growth). Let’s elaborate a little on this idea of allometry. If two quantities are related by a power law,
y
∝
x
a
say, then
a
is called the
scaling exponent
. If
a
= 1 the quantities exhibit
isometric
scaling, for example, change of size without change of proportion (this is also referred to as
geometric similarity
). Allometry is often expressed in terms of a scaling exponent based on the mass
M
of the object of interest. Thus an isometrically scaling object (such as a cube of side
L
) would have all volume-based properties change in proportion to
L
3
, or equivalently as mass to the first power, that is,
V
∝
M
; all surface area-based properties change in proportion to
L
2
, or
M
2/3
, and all length-based properties change in proportion to
L
, or
M
1/3
. Another example worth mentioning is
Kleiber’s law
: an organism’s metabolic rate is proportional to
M
3/4
; whereas breathing and heart rates are both proportional to
M
1/4
(see West 1999 for more details).
In 1949, Harvard linguist George Zipf proposed [
31
] that city sizes (along with many other things) follow a special form of the distribution where
a
≈ −1. This has become known as
Zipf’s law
: the frequency of cities within a given size is inversely proportional to their rank. However, as pointed out by Batty
and Longley
[
1
], most of the work on city-size distributions neglects any spatial structure that exists within cities. By this they mean that cities as measured by populations or incomes, among other measures, are considered as points with their sizes reflecting the competition
between
cities as opposed to competition
within
the city. In other words (and as illustrated by Zipf’s law) there are
a small number of large cities and a large number of small ones because there are not the resources and demand to sustain many large cities. Zipf’s law is empirical in that it has been observed in data taken from a wide range of cities in space and time, but so far no entirely satisfactory theoretical explanation has been found for it. Such an explanation must surely establish the basis for the observed organizational principles that appear to be replicated across such wide spatial and temporal scales.
But it does seem that similar principles must be at work
within
cities, based on microeconomic factors such as population density, rent, employment, transportation costs, and so on. Of interest then, in this context are the constraints that geometry imposes on “density” and “nearness” in a city; a plausible approach by virtue of the fact that sizes of structures indirectly reflect population and employment “volumes.” In particular, as buildings grow in size, their shape must change to enable them to function efficiently, and the scaling exponent
a
is related to the governing allometric “law.” Examples include the cost of heating (or cooling) a building; crudely speaking, heat loss will be proportional to the surface area of the building, but the amount of heat required to maintain equable temperatures will depend essentially on the volume of the building. Natural lighting provides another illustration; this will depend on the surface area of the building, but since the area changes with size more slowly than does the volume, the shape of the building must change as it grows to accommodate the requisite increase of natural illumination. In fact, it has been argued that cities yield some the best examples of
fractals
(see below). It is possible to fit power laws and allometric scaling relations to several geometrical properties of buildings—perimeter, area, height, and volume—using a large database of buildings in Greater London, which contains some 3.6 million “building blocks”!
So what might be these basic scaling laws for cities? We mention perhaps just enough to whet the reader’s appetite for more advanced discussions of this topic. (The reader may wish to consult
Appendix 9
for a short introduction to fractals.) Modifying somewhat the notation in that Appendix to fit the present context, we identify the number of parts composing an object, their total length and area at a given scale
a
as
N
,
L
, and
A
, respectively. Specifically, they are defined by the relations
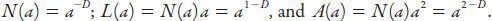
T
ABLE
18.1.
Estimated fractal dimension
D
for several cities
City
D
Beijing (1981)
1.93
Berlin (1945)
1.69
Boston (1981)
1.69
London (1981)
1.72
Los Angeles (1981)
1.93
Melbourne (1981)
1.85
Mexico City (1981)
1.76
Paris (1981)
1.66
Rome (1981)
1.69
Tokyo (1960)
1.31
If
A
(
R
) is the area of the object, considered to be constant regardless of the scale of resolution, then it is reasonable to define the density as

If we allow the scale to become finer and finer, so that as
a
→ 0 (assuming 1 <
D
< 2), then
N
(
a
) → ∞,
L
(
a
) → ∞,
A
(
a
) → 0, and
ρ
(
a
) → 0. In particular, the perimeter becomes infinite as the scale becomes finer. This is an important characteristic (among others) associated with fractal behavior.

